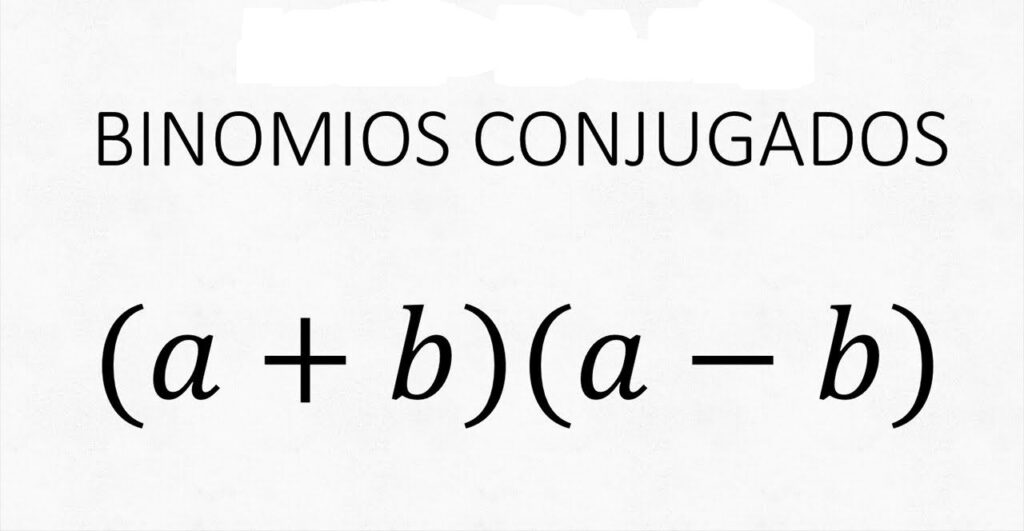
Un binomio conjugado es una expresión matemática que consiste en dos términos que se multiplican, y que se diferencian sólo por un signo. El primer término es una variable y el segundo es un número. El término variable y su conjugado se suman y se multiplican. Ejemplo de binomio conjugado es (x+3)(x-3).
Características
- Son expresiones matemáticas que constan de dos términos.
- Los dos términos se multiplican entre sí.
- Los términos se diferencian sólo por un signo.
- El primer término es una variable y el segundo término es un número.
- El producto de un binomio conjugado es igual al producto de la suma y el producto de la diferencia de los términos.
- El segundo término en un binomio conjugado es el conjugado del primer término.
- El producto de un binomio conjugado es siempre un polinomio de segundo grado.
- El coeficiente del término cuadrático en un binomio conjugado es siempre 1.
- El coeficiente del término lineal en un binomio conjugado es igual a cero.
- El coeficiente del término independiente en un binomio conjugado es igual al producto del segundo término y su conjugado.
Importancia
La importancia del binomio conjugado radica en su utilidad en el álgebra y en otras ramas de las matemáticas, como la trigonometría y el cálculo. Algunas de las aplicaciones más importantes son:
- Factorización de expresiones: El binomio conjugado se utiliza para factorizar expresiones cuadráticas. Al multiplicar dos binomios conjugados, el término del medio se elimina y se obtiene una expresión que se puede factorizar con mayor facilidad.
- Simplificación de fracciones algebraicas: El binomio conjugado se utiliza para simplificar fracciones algebraicas que tienen un denominador con una suma o resta de términos. Al multiplicar el numerador y el denominador por el binomio conjugado del denominador, se elimina el término del medio y se obtiene una fracción más sencilla.
- Identidades trigonométricas: El binomio conjugado se utiliza en la trigonometría para demostrar identidades trigonométricas. Por ejemplo, la identidad sen²θ – cos²θ = -cos2θ se puede demostrar utilizando el binomio conjugado.
- Cálculo: El binomio conjugado se utiliza en el cálculo para calcular límites y derivadas de funciones que contienen radicales en el denominador. Al multiplicar el numerador y el denominador por el binomio conjugado del denominador, se elimina la raíz cuadrada y se puede calcular el límite o la derivada con mayor facilidad.